Neural Networks from Scratch

Hi there, I’m a junior student from Shanghai JiaoTong University(SJTU). In my sophomore year, I started to learn about machine learning with a try of using Support Vector Machine (SVM) to classify credit card digits, something like the MNIST TASK. Then I joined ADAPT and began my research work on NLP.

Within the NLP domain, many statistic methods work quite well, giving astonishing results on the basic tasks, chunking (which is especially important in Chinese), Part of Speech tagging (POS) and Named-Entity recognition (NER). Models like Hidden Markov Model (HMM) and Conditional random fields (CRF) can give you a glimpse.

These days, I was attracted by the awesome performance of Deep Learning in NLP, which utilizes Neural Networks Models. I’ll try my best to give an overlook over the Neural Networks stuff. On my own experience, the mathematic things sometimes distract me from the intuitive of how Neural Networks works. Thus, in this blog, there will only be some “baby math”, as Prof. Chris Manning named in CS224n.

Part of this blog overlaps with the great blog from Andrej Karpathy, which definitely worth reading. But I’ll try to give you something more concrete about backpropagation by implement a linear regression model, and illustrate some examples and applications of Neural Networks in NLP, including word embedding and character-level language model.

Let’s start!

Chapter 1: Vanilla Neural Networks

At the first glance of the Neural Networks architecture, I wonder how it works so brilliantly. It seems non-sense that several layer of mathematic computation can simulate human brain, one of the most complicated creature in the world, even a little.

Human Neurons

Let’s turn to how our brain works to get an intuitive idea.

A brain neuron and its main components. Image credit: Quora

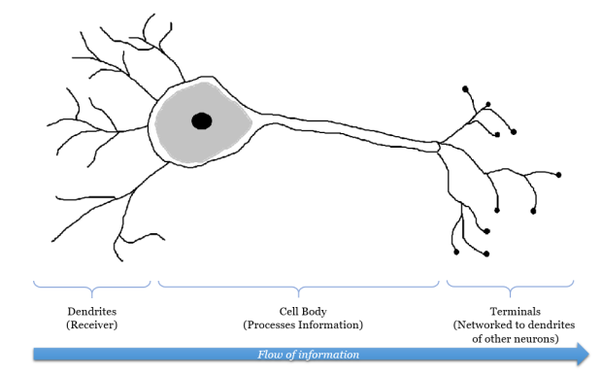
Our brain has a large network of interlinked neurons, which act as a highway for information to be transmitted from point A to point B. When different information is sent from A to B, the brain activates different sets of neurons, and so essentially uses a different route to get from A to B.

At each neuron, dendrites receive incoming signals sent by other neurons. If the neuron receives a high enough level of signals within a certain period of time, the neuron sends an electrical pulse into the terminals. These outgoing signals are then received by other neurons.

Credit: Quora answer by Annalyn Ng (Quote part of her answer, click if you are interested, which I recommend you to do.)

Modeling Human Neural Network

Let’s recap what we can learn from last section:

• Information is sent between neurons.
• A neuron can be activated when received certain signal.

Here I’ll introduce a vanilla Neural Networks Model, with a vector of length 8 as input, a hidden layer of 4 neurons, and a vector of length 3 as out put, the NN model can be trained as a image classifier for 3 tags.

Vanilla Neural Network architecture, with one hidden layer

You can image that if you feed a picture involving animal into the network, it can output a tag of "cat" or "dog".

`W` and `b` are parameters of the model, which can be learned by training.

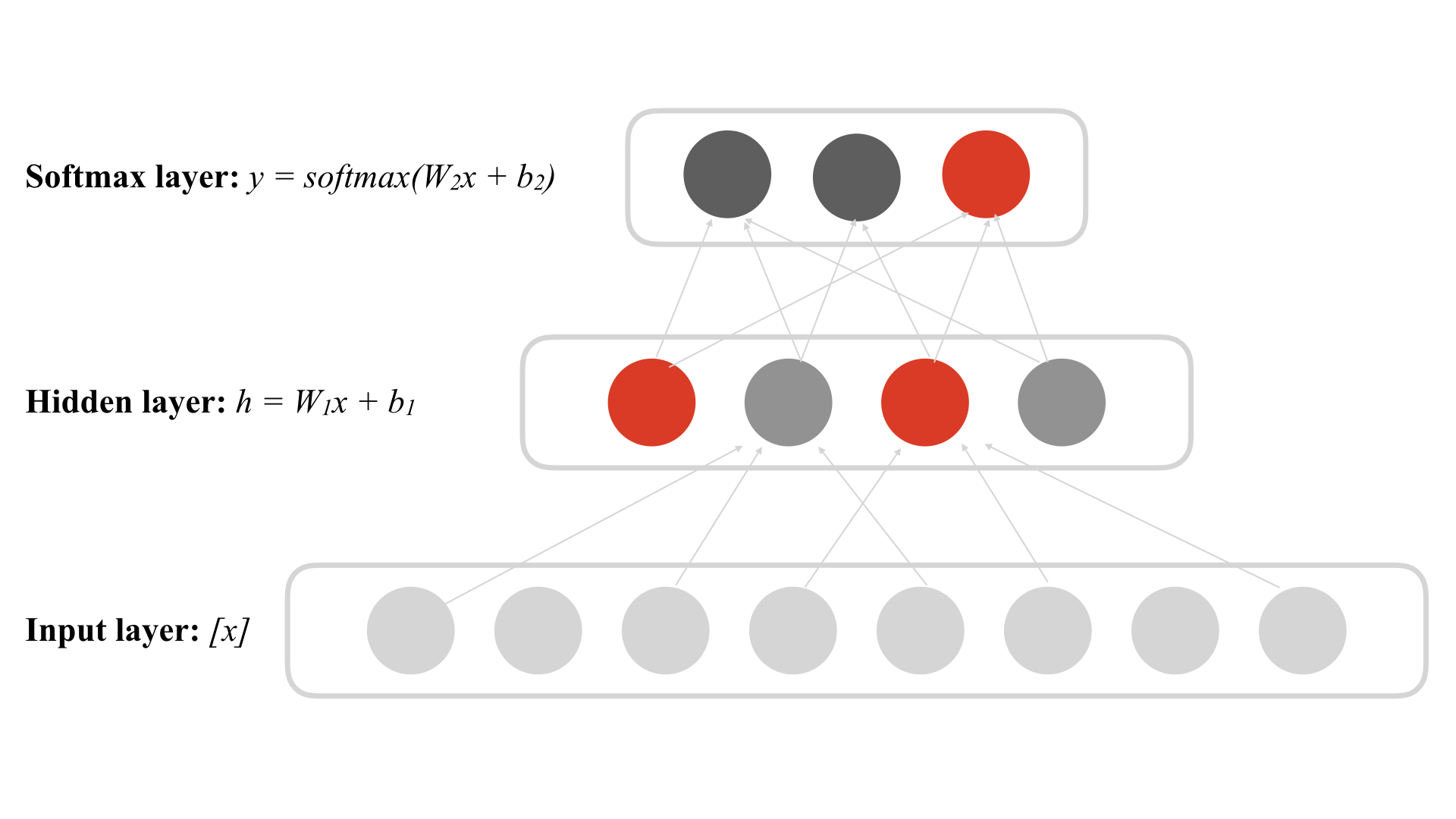
As you can see in the picture, when facing an input of a cat picture, the first and third (from left) neurons are activated (red), and then, these neurons send signal to the output layer and get a “cat” output.

Thinking about our brain do the same thing when we see a cat, some neurons are triggered and we find out that it is a cat!

This is the intuitive I see from the Neural Networks, though it is a simplified and idealized model just like most of the models in the world, it has the potential to improve machine intelligence.

Practically, Neural Networks contains millions, even billions of neurons, each be sensitive to certain input, automatically learn features and representations, thus obtains intelligence.

Till now, I believe that you have obtained an intuitive idea about how Neural Networks works. Then I’ll introduce how data flows from input to out, a feedforward process, and how the weight matrix and bias are trained, a backpropagation process.

Feedforward

The feedforward process is straightforward, you can treat it as a function, feed it and it will give an output.

Backpropagation

The backpropagation process is to tune the parameters, e.g. W and b, to fit the training data, minimize the total loss. I’ll take a simple linear regression model as an example, to illustrate how backpropagation works with Stochastic Gradient Descent (SGD).

Consider a network take a scalar x as input, and output y = ax + b. If we train the model on training set:

The model will soon fit the function $y = -x + 5$, with quadratic loss function and SGD.

Let’s take the derivative first!

As you may acknowledge, Chain Rule is the key tool we should utilize. Backpropagation propagates through the chain rule from back to front.

Time to code! A toy implementation with pure Python:

X = [1, 2, 3, 4] # training set
Y = [4, 3, 2, 1]
w = 0 # initiate parameter as 0
b = 0

lr = 0.1 # learning rate
assert len(X) == len(Y)
for i in range(200):
    total_loss = 0
    for j in range(len(X)):
        x = X[j]
        y_ = Y[j]

        y = w * x + b # feed forward
        loss = (y - y_)**2 / 0.5
        total_loss += loss # accumulate loss

        dy = y - y_ # calculate derivative
        dw = dy * x
        db = dy * 1

        w -= lr * dw # backpropagation
        b -= lr * db
    print("After iteration {}, loss: {:.2f}. y = {:.2f}x + {:.2f}".format(i, total_loss, w, b))

Output:

After iteration 0, loss: 44.47. y = -0.10x + 0.34
After iteration 1, loss: 39.21. y = -0.16x + 0.68
After iteration 2, loss: 33.80. y = -0.22x + 0.99
After iteration 3, loss: 29.14. y = -0.28x + 1.27
After iteration 4, loss: 25.12. y = -0.33x + 1.54
After iteration 5, loss: 21.66. y = -0.38x + 1.79
After iteration 6, loss: 18.67. y = -0.42x + 2.02
After iteration 7, loss: 16.10. y = -0.46x + 2.23
After iteration 8, loss: 13.88. y = -0.50x + 2.43
After iteration 9, loss: 11.96. y = -0.54x + 2.61
After iteration 10, loss: 10.31. y = -0.57x + 2.78
...
...
After iteration 51, loss: 0.02. y = -0.98x + 4.89
After iteration 52, loss: 0.02. y = -0.98x + 4.90
After iteration 53, loss: 0.02. y = -0.98x + 4.91
After iteration 54, loss: 0.02. y = -0.98x + 4.92
After iteration 55, loss: 0.01. y = -0.98x + 4.92
After iteration 56, loss: 0.01. y = -0.99x + 4.93
After iteration 57, loss: 0.01. y = -0.99x + 4.93
After iteration 58, loss: 0.01. y = -0.99x + 4.94
After iteration 59, loss: 0.01. y = -0.99x + 4.94
After iteration 60, loss: 0.01. y = -0.99x + 4.95
...
...

Let’s recap what we have learned:

• An intuitive idea of how Neural Networks models human brain and how it works
• Feedforward process acts like a simple function
• Backpropagation utilizes Chain Rule to calculate derivative of each parameter, updates the parameters and minimize the loss

Application: Word Vector

It is hard for us to encode words so that computer can use and meanwhile, keep the “meaning”. A common way to utilize the “meaning” is to build a synonym set or hypernyms (is-a) relationship set, like WordNet. It’s useful but largely limited, limited to the relation set and the vocabulary set.

If we regard words as atomic symbols, we can use one-hot representation to encode all the words. Such representation also suffers lack of “meaning” and flexibility (influence all words when adding new words), and memory usage (13M words in Google News 1T corpora). The inner production of 2 different word vector is always 0, means nothing.

However, researchers came up with an idea that we can get the meaning of a word by its neighbors.

“You shall know a word by the company it keeps” (J. R. Firth 1957: 11)

It reminds me of the years I was new to English. As a non-native speaker, I always look up in a dictionary when meeting a unknown word, but teachers said that “Never look up at first glance! Guess its meaning from the context first!”.

Here’s an example about word and context from CS224n:

government debt problems turning into banking crises as has happened in
   saying that Europe needs unified banking regulation to replace the hodgepodge

The words in the context represent “banking” !

Recent years, with the proposition of Mikolov et al., distributed representation of word can be trained fast and successfully captures word’s semantic meaning.Till now, there are 3 main models to train word vectors:

1. word2vec
2. GloVe
3. FastText

I’ll introduce the word2vec model, for these 3 models are almost the same. GloVe takes statistic feature into account, and FastText predicts tag instead of words. I won’t go detail to the training tricks, such as negative sampling, hierarchical-softmax, to name just a few.

The key idea of word2vec is:

Predict between every word and its context words.

So obviously there are two algorithms:

1. Skip-Gram (SG): Predict context words given target word
2. Continuous-Bag-Of-Words (CBOW): Predict target word given context words

As shown in the diagram, CBOW takes context word as input and predicts the target word, SG generates the context-target pairs and predicts one context word given the target word.

It’s time to dive deep into the skip-gram model. The diagram below is a clear representation from CS224n.

Skiip-Gram model

Image credit: CS224n

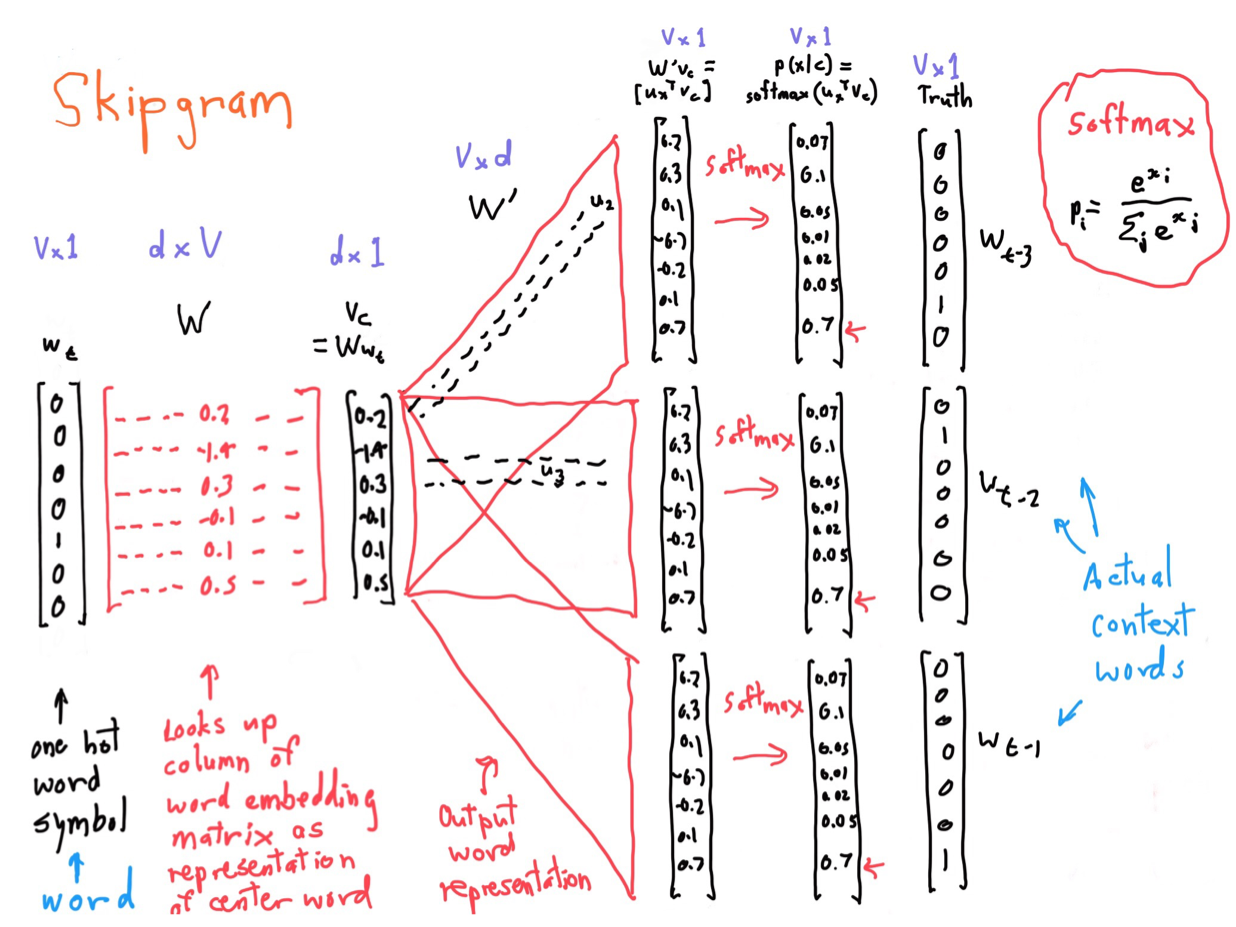
Define the notation:

• $V$ vocabulary size
• $d$ dimension of word embedding
• $w_\epsilon$ one-hot representation of the word
• $W$ word embedding matrix
• $V_c$ word vector of a word
• $p(x{\vert}c)$ the probability of context word x given center/target word c

We take one-hot representation $w_\epsilon$ to encode a word in dictionary, then look up in the word embedding matrix $W$ for the representation $V_c$, using the dot production $V_c = Ww_\epsilon$. After that, another dot production $W^{'}V_c$ is used to calculate the hidden representation of output word, then utilize $softmax$ to get the probability representation of output word. In the training, we have the truth answer, so we can calculate the loss and then backprop to tune the model parameters ($W, W^{'}$).

Given a vector $x = [x_0, x_1, ..., x_{n-1}]$:

Well, a little more explanation of the diagram. The 3 vectors at the end of the model represents all the context words for one center/target word. It stands for the several context-target pair we generates from the training corpora, doesn’t mean that we predicts several context words on one feedforward.

If you are interested in how to code a word2vec model, here is a toy example with PyTorch.

Chapter 2: Recurrent Neural Networks

TODO